Zusammenfassung auf Polybox
Kontakt:
- barski
- email: pbarski@student.ethz.ch
- discord: phil1331
- notizen: https://polybox.ethz.ch/index.php/s/p0Ws9UqWdadlGkQ
- Dan Philipp
- norizen: https://n.ethz.ch/~philippda/
- cheatsheet: https://n.ethz.ch/~philippda/DiskMath_Spick
- alle Übungsstunden: [[Übungsstunden_mit_Lösungen.pdf]]
Lernmaterialien:
- Skript
- Übungen
- https://discmath.ch
- alte Prüfungen
Struktur:
- Pseudo-Kapitel
- Logik, Einführung in Beweise !!!
- Funktionen, Mengen, Relationen, Abzählbarkeiten
- Zahlentheorie
- Algebra
- (Rigorose) Logik
Mathematische Aussagen und Formeln
#timestamp 2024-09-23
mathematische Aussagen ("Propositionen"): Aussagen, denen man eindeutig ein "Wahr" oder "Falsch" zuordnen kann (nach der Mathematik)
| Def: ( wahr) und es gibt einen Beweisschritt, sodass T aus S wahr wird - und, oder
Bsp:
Formeln:
ist Formel
Für
Bsp: Prove or disprove
- nicht äquivalent bei 3x 0 ->
- Lösung: Consider the assignment of propositional symbols that appear in F or g (
). Then, F yields truth value 0 and g yields truth value 1. By definition, this means F and g are not equivalent.
Umformungen (Äquivalenztransformation):
#timestamp 2024-09-30
Wichtig: (Umformungen)
- Immer nur einen Schritt pro Umformung ändern
- z.B.
ist nicht erlaubt, da nicht definiert
Prädikatenlogik / First-Order Logic
Prädikate:
Formeln:
Interpretation:
- Universum, Zuweisung (variablen, prädikate, ...)
Alle natürlichen Zahlen sind grösser gleich a
Twin-Prime Conjecture
"es gibt unendlich viele "Primzahlen": p, q, sodass p-q=2
- prime (p)
Äquivalenzumformung
2024-10-07
if -> normalerweise Implikation
direkter Beweis
indirekter Beweis
-
Schritt: S und T definieren
ungerade
und ungerade -
falsch a oder b gerade
Wir nehmen o.B.d.A (ohne Beschränkung der Allgemeinheit) an, dass a gerade ist
Somit ist die Aussage durch einen indirekten Beweis bewiesen.
Modus Ponens
- passende Aussage
- Wir beweisen, dass
wahr ist - beweisen
Wiedersprichsbeweis
- passende Aussage
falsch beweisen - annahme
falsch, zeigen dass unter annahme wahr
- S und T definieren
T soll eine unabhängig von S falsche Aussage sein
Wir haben einen Widerspruch und somit folgt, dass
Case distinction
- verschiedene Fälle, die eintreten
- beweisen, dass immer mindestens ein Fall eintritt
- jeden Fall beweisen
teilbarkeit durch drei:
- es gibt nur drei fälle: n, n+1, n+2
Soundness of proof pattern
- pattern
sound, wenn damit nur wahre Aussagen zeigen können
- Beweisenden Aussage formel
zuordnen - den schritten im proof pattern formel
zuordnen - zeigen
z.B. indirekter Beweis:
z.B. Prüfungsaufgabe
proof pattern:
- A or B true
is false
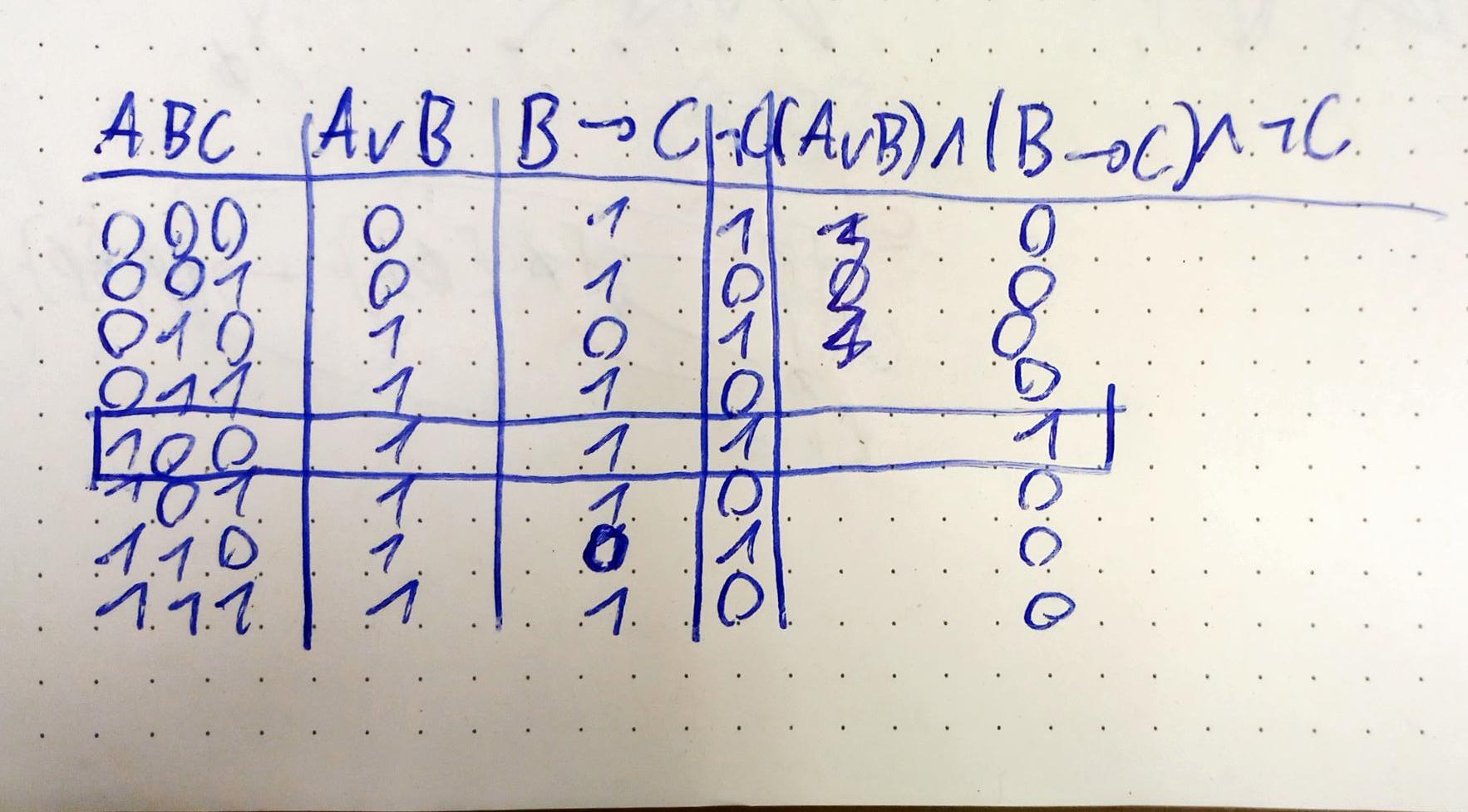
In the truth table we see that
2024-10-14
Mengenlehre
- jede Menge is Teilmenge von sich selbst
- eine Leere Menge ist immer eine Teilmenge, aber nicht immer ein Element
- für eine endliche Menge A gilt:
- für eine endliche Menge A gilt:
ist Kardinalität, d.h. die Anzahl Elemente
Bsp:
gleichheit von Mengen beweisen/wiederlegen
Bsp: Beweise oder widerlege
Für alle Mengen
Wiederlegen:
- Gegenbeispiele (z.B. alle Mengen gleichsetzen
oder Beispiel finden (Venn-diagram zeichnen))
- Abschlusssatz: Da
gilt nicht
Beweisen:
- evtl. zahlenbeispiel
- Lösungswege
- in logik umwandeln -> umformen -> zurück in Mengen
- theorem 3.4: direkt mit Mengen umformen
: und seperat beweisen: - Lemma 3.2:
Bsp Lösungsweg 1
Beweise oder wiederlege:
Für alle Mengen
Seien
Somit gilt
Folgerungsschritte gelten in beide Richtungen. (Der erste schritt ist keine äquivalenzumformung da definition verwendet wird, um logikformel zu bekommen, danach auch äquivalenzumformung möglich zu schreiben)
2024-10-21
Relationen
-
Eine Relation
von einer Menge auf eine Menge ist eine Menge: -
heist ist ein Relation zu , man schreibt auch -
auf Relation können wir somit Mengenoperatoren anwenden:
- z.B.
- z.B.
-
Komposition: Für
ist die Komposition
Bsp:
Komposition:
Eigenschaften von Relationen
Wir betrachten eine Relation
- Reflexiv: Für alle
gilt: - Symmetrisch: Für alle
gilt: - Antisymmetrisch: Für alle
gilt: - Transitiv: Für alle
gilt:
Zu relationen gibt es immer eine Prüfungsaufgabe
Äquivalenzrelation
ist
- reflexiv
- symmetrisch
- transitiv
notation:
Bsp:
-> ist auch transitiv, weil nie erfüllt, siehe:
Graph:
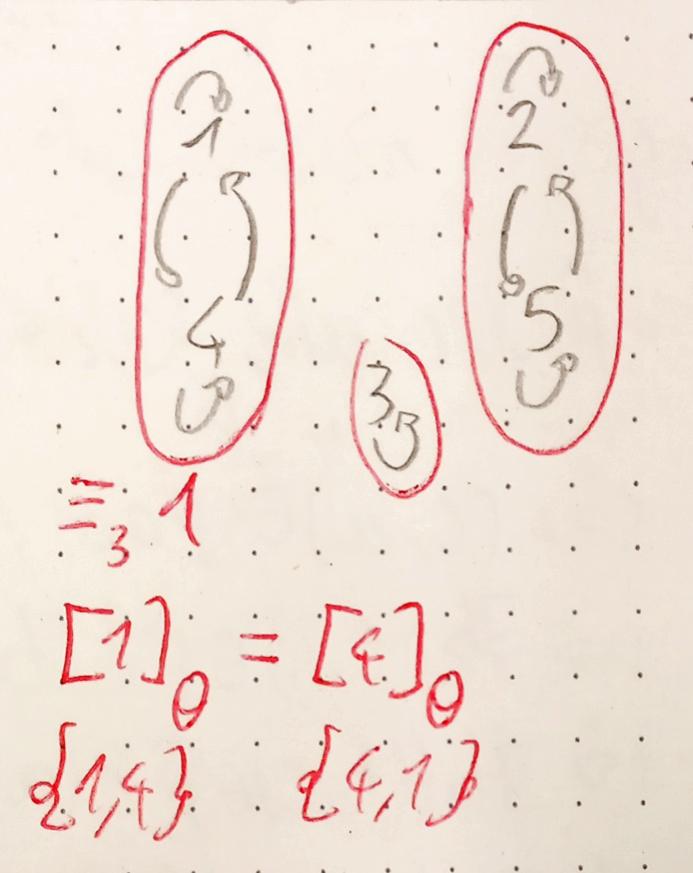
-> antisymmetrisch
Equivalence relation proof:
- [[2024_10_21 17_48 Office Lens.pdf]]
Wir nehmen einen Teilmengenbeweis an
Sei
1.Fall:
2.Fall:
Da
2024-10-28
5.5)c) Nachbesprechung
Hasse-Diagramme
- Wir betrachten Posets (
) - Zwei Elemente
sind vergleichbar, wenn oder ist minimales Element, wenn kein mit existiert - (kein Pfad nach unten im Hasse Diagramm)
ist kleinstes Element, wenn für alle - (mit allen Elementen verbunden im Hasse-Diagramm, muss nicht existieren)
Funktionen
- von Domain
zur Codomain
- Es muss gelten:
totally defined: - alle Zahlen erreichbar
well-defined: - nur ein ergebnis pro zahl
- Eigenschaften: Eine Funktion
ist - Inkektiv: Wenn
, dann gilt - Surjektiv: Für jedes
gilt für ein - Bijektiv: injektiv und surjektiv
- Inkektiv: Wenn
Bsp:
- injektiv
- surjektiv
-> funktionert nicht wenn
Bsp
-
nicht injektiv: (mehrere zahlen auf gleiches element im Codomain)
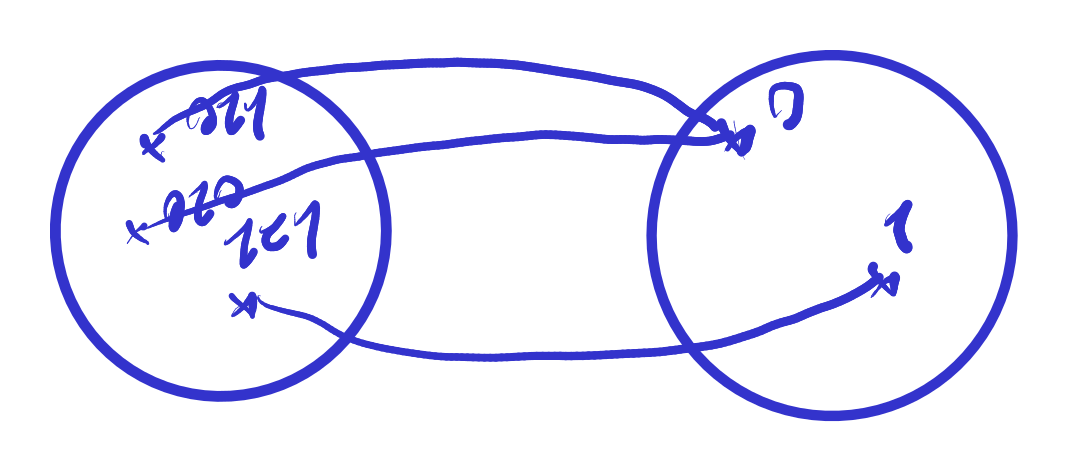
, aber -
surjektiv, da
-> jedes Element erreicht
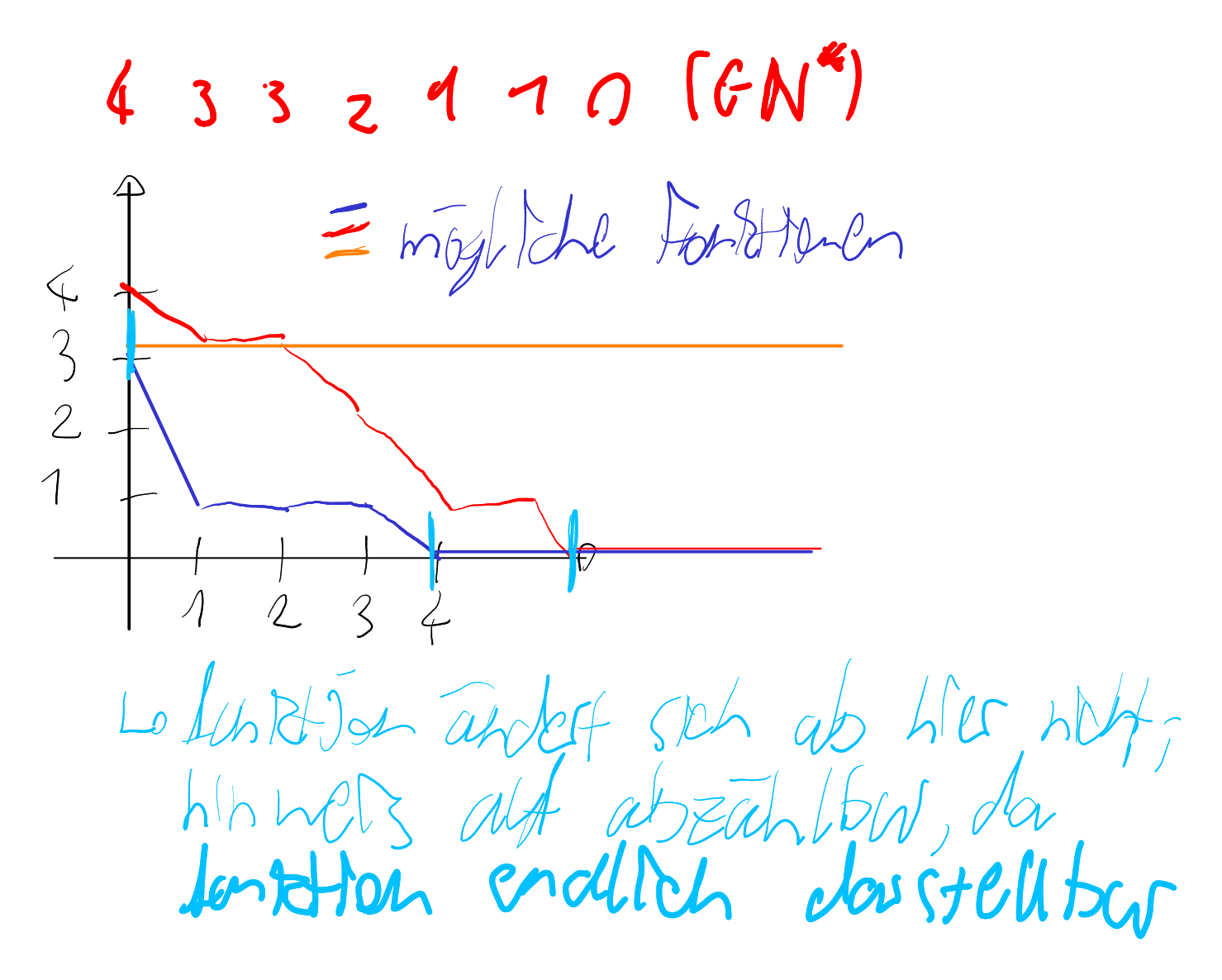
Abzälbarkeit
- Wir wollen zeigen, dass eine Menge A abzählbar ist:
- Wir definieren eine Funktion
, wo eine abzählbare Menge ist (z.B. ) - Zeige, dass wirklich
gilt für alle - Wir zeigen, dass diese Funktion injektiv ist
- Wir definieren eine Funktion
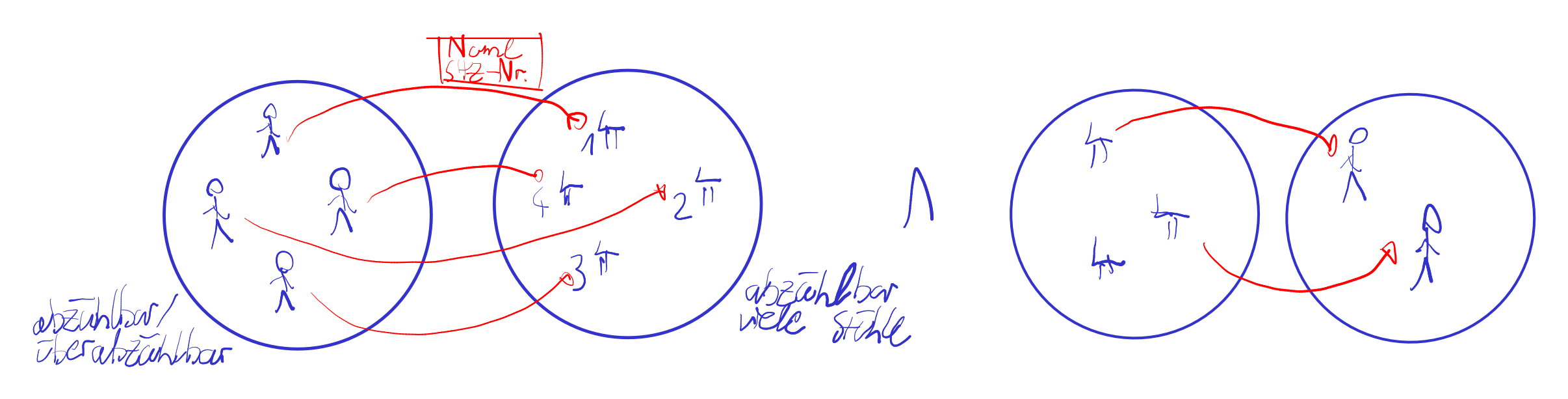
eine solche Aufgabe kommt normalerweise an Prüfung, gibt viele Punkte
2024-11-04
Nachbeschrepchung Bonus
- keline Begründunge, warum eine Injektion zu finden die uncountability beweist
- alle Schritte genau asführen
- Achtet auf die Domain/Codomain der FUntionen in
Aufgabe
Beweise oder widerlege
Wir definieren
Sei
Zeige
Sei
Da
g injektiv:
Sei
Somit gilt
Für alle
Modulo rechnen
der Rest, wenn wir n durch m teilen - Bsp:
- Bsp:
- Für Addition und Multiplikation gilt:
- Formale Definition:
- wichtig für beweise
Bsp
Bsp
oder
-> für diesen Aufgabentyp zählt nur die Lösung
Bsp
Number Theory
Thoerem 4.6 Jede natürliche Zahl kann eindeutig in ein Produkt aus Primzahlen zerlegt werden
grösster gemeinsamer Teiler von und kleinstes gemeinsames Vielfaches von und
Bsp
Euklidischer Algorithmus
- Ziel:
berechnen
- wir teilen die grössere Zahl durch die kleinere und notieren den Rest
- Wir wiederholen dies, bis eine der Zahlen 0 ist
- Die andere Zahl ist dann der
Bsp
=>
-> relativ häufiger aufgabentyp an prüfung
Bsp
Zeige, dass keine
Wir betrachten
Da
welches modulo benutzen -> ausprobieren
Ideal
- Bsp
- Bsp
- Bsp
- Mengenbeweis, da Menge !!!
- Bsp
Multiplikative Inverse
hat nur eine Lösung genau dann wenn
Die Lösung können wir mit dem erweiterten euklidischen Algorithmus berechnen.
Bsp
Berechne die multiplikative Inverse von
-> euklidischer Algorithmus
Chinese Remainder Theorem
Wir haben mehrere modulare Kongruenzen mit einem x, das wir
suchen:
Wichtig: Die Moduli (2,5,7) müssen paarweise teilerfremd sein.
Dann gilt: Es gibt eine eindeutige Lösung für x mit
Diffie-Hellman Protokoll
Funktionsweise des Protokolls auf das Cheatsheet aufschreiben
#timestamp 2024-11-11
2024-11-11
Algebra
Algebra:
Monoid
ist assoziativ ist neutrales element
Gruppe
- G1
ist assoziativ - G2:
ist neutrales Element - G3 Jedes
hat ein inverses element
Eine Gruppe ist abelsch, wenn
Subgroups
Für
for all a,b forall
Lagrange: Die Ordnung einer Subgroup teilt die Ordnung der Gruppe
Morphisen
Ein Homomorphismus ist eine FUnktion
Wenn diese Funktion zusätzlich bijektiv ist, ist es ein Isomorphismus. Mann schreibt dann
Isomorphismus beweisen
Zu beweisen:
- Funktion
finden - ...
Zyklische Gruppen
- Für eine Gruppe
und ein ist die Gruppe generiert von :
- Einge Gruppe ist zyklisch, wenn es ein
gibt mit
Zyklische Gruppen
Wir wollen einen Generator einer zyklischen Gruppe
- Gruppenordnung
berechnen - Die Ordnung jedes Elements muss nun ein Teiler der Gruppenordnung sein
- Wenn für ein
gilt , es ist ein Generator - Somit finden wir die Generatoren durch Ausprobieren
Gruppenordnung
anzahl Elemente
Ordnung von Elementen
Bsp
#timestamp 2024-11-18
Isomorphe und zyklische Gruppen - Übersicht
slides may be outdated
![[Übungsstunde 9.pdf]]
Einheiten und Nullteiler
see above
- für endliche Gruppen gilt: Jedes Element ist entweder Einheit, Nullteiler oder 0.
(Einheiten: Alle Teilerfremden Elemente (?))
Polynome in Ringen
see above
Körper
see above
- kommutative Ring mit
mit ist abelsche Gruppe ist abelsche Gruppe
2024-12-02
#timestamp 2024-12-02
![[Übungsstunde 11.pdf]]
Beweissysteme
- complete: zeigen, dass es für beliebiges
gültigen Beweis gibt - nicht complete: gegenbeispiel
Bsp:
(kommt so nie vor)
Bsp
-> muss nicht sound sein
2024-12-09
#timestamp 2024-12-09
Logic
forms: menge aller formeln
- Syntax: Alphabet
, Forms - Semantics: For
Forms - free
- Interpretation
"assigns free symbols" suitable for if it assigns all free symbols in .
(write for )
- free
Bsp
Interpretation
z.b.
- mit def 6.16 auswerten
def 6.9 For
def 6.10-13
is satisfiable if for some interpretation . is tautology if for all interpretations . formulas. is log. consequence of (write ), if for any suitable for bot :
How do we prove:
| Take arb. suitable for both. Show - oft direkt, manchmal indirekt
| Counterexample: find suitable for both s.t. | Show and | Show or is taut | Take arb. , show is not a taut. | Construct s.t. is satisfiable | Construct s.t. is not satisifiable | Take arb. , show
Pred. logic
- Syntax:
, , (vars, facts, predicates) - possibly free symbols
shows arity - wir quantifizieren nur über variablen ("first-order logic")
- term variables are terms,
are terms (for terms -> recursive def) - werden Universumswerte zugewiesen (siehe semantik)
- forms:
, , , , , - for
formulas, terms, - werden Wahrheitswerte zugewiesen (siehe semantik)
- for
- Semantics:
: non-empty set (universe) - write
- write
: ( - write
- write
: - write
- write
- write
- write
free symbols:
| PropL | Pred L |
|---|---|
| atoms (atomic formulas) | |
| assigns |
|
For terms
- jeder variablen wird wert zugewiesen, Funktion/term wird dann auf diese Variablen angewendet
For formulas:
def 6.16
und or
where
Bsp
einfache Prüfungsaufgabe
Find a model for
- freien Symbole:
-> mindestens sie müssen definiert werden - Universum wählen
Bsp (nicht eindeutig)
- verify (in der Prüfung nur kurze Begründung):
-> def. einsetzen
Bsp
Prove for any formula
Let
Assume
#todo: why is step 2 incorrect for
Bsp
Prove:
Let
Assume
- case 1:
appears free in : since is suitable for , is defined. implies
- case 2:
doesn't appear free in : (nicht frei oder kommt gar nicht vor) - Then
for any implies
- Then
in either case,
``
(
In diesen beweisen kommt Fallunterscheidung um freie Variablen oft vor
-> aufpassen! wenn wir nicht wissen, ob freie variable vorkommt, immer case distinction machen
Bsp
Disprove: For any formula F:
We disprove the claim by giving a counterexample :
Let
Then
On the other hand, since
for some
2024-12-16
Resolutionskalkül
Bsp
...
- nur einmal anwenden möglich
-> nur möglich: